Memory Learning, Model Titans (Behrouz et al, 2024)

“Titans: Learning to memorize at test time. arXiv preprint arXiv:2501.00663” This paper (Behrouz et al, 2024) [1] aims to build a memory learning model that is efficient, uses less memory, and learns and predicts more. Neural learning is the basis of memory-based learning. Forgetting is important too, and too much forgetting can lose essential data about the input. Its base is concepts in attention-layer memory formulations relating to associative memory, and it conceptualizes surprise in memory as a basis for understanding and moving forward. In addition to input and memory, the authors suggest using Np number of persistent memories. These are learnable but input-independent parameters to act as task-related memory. The experimental results are promising.

The details are from (Behrouz et al, 2024), given in reference [1] at the end of the article.

Summary– We have “attention mechanism” as the basis, let’s first understand that. A momentum-based equation for memory is derived. The terms in the momentum equation for memory are given in Section 4 below. Before that, we show that we can write the softmax given in Section 1 as a recursive memory model in Section 2. Memory is written in the form of momentum and surprise. Loss function is defined as key-value access to memory and is reduced to efficient matrix computation. Momemtum memory is simplified. Finally, the model is defined by the Attention layer.

Index:

1. Recurrent softmax in linear form.
2. Softmax in recursive memory form.
3. Memory as a function of surprise in data.
4. Attention Mechanism in the form of momentum.
Past surprise is separated from momentary surprise. 
5. Loss function as key-value access to memory.
6. Loss function as matrix computation.
7. Momentum memory simplified.
8. Titans model differ in the last step.

1— Recurrent softmax in linear form.

2— Softmax in recursive memory form.

The following derives memory as associative memory formulations Reference [1]:

3— Memory as a function of surprise in data.

4— Attention Mechanism in the form of momentum

— Past surprise is separated from momentary surprise.

The intitial memory can be lost or gained in right manner by using right parameters.

5— Loss function as key-value access to memory.

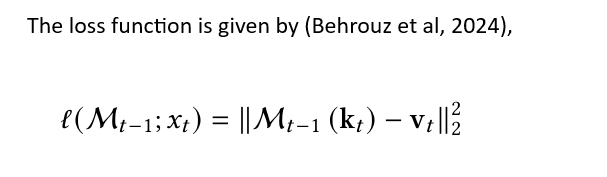
6— Loss function as matrix computation.

The equations can be simplified as follows.

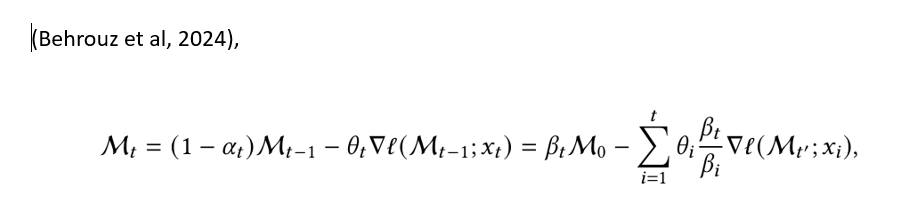
7— Momentum memory simplified.

In addition to input and memory, the authors suggest using Np number of persistent memories.

8 — The model is now defined as follows.

This is about attention and learning. In addition to input and memory, the authors suggest using Np number of persistent memories. These are learnable but input-independent parameters that serve as task-related memory; they can be concatenated as follows.

𝑥_new = [𝑝1 𝑝2 … 𝑝𝑁𝑝] || 𝑥

𝑦 =M(𝑥_new),

And the output is,

𝑜 =SW-Attn(𝑦), SW-Attn is sliding window attention

References

[1] Behrouz, A., Zhong, P., & Mirrokni, V. (2024). Titans: Learning to memorize at test time. arXiv preprint arXiv:2501.00663.