Generalized Traveling Salesman Problem Using Genetic Algorithms

Here in this article, we will see how to use Genetic Algorithms (GA) to solve the Generalized Traveling Salesman Problem, or G-TSP for short.

Question. So what is the Generalized Traveling Salesman Problem?

The aim here is to choose a path from a cluster of cities that covers all clusters and has the minimum cost. It is a TSP problem on a cluster of cities wherein one city from each cluster is selected to take part in the process.

Consider there are m clusters and each of the m city clusters has ni cities. So there are clusters c1, c2,…, cm, and each cj have nj clusters.

Question. Why to use GA to solve G-TSP?

This is so because the computation complexity of such a problem is very high. This is equal to,

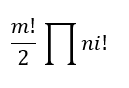
Hence, methods which use heuristics and can solve combinatorial problems can be used to solve G-TSP.

Question. Explain G-TSP.

Let us write the mathematical formulation of G-TSP. This is taken from reference [1]

The constraints are given as follows [1]:

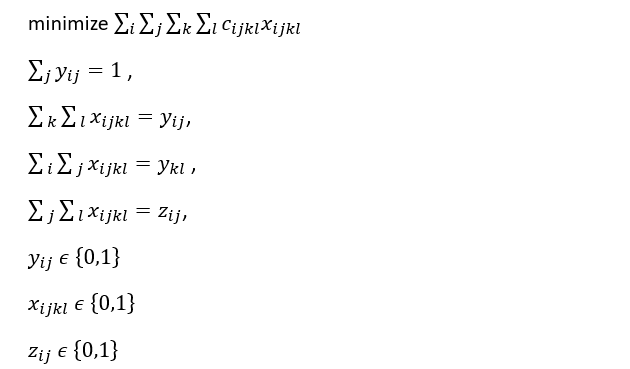
The first equation makes sure that only one city is selected per cluster. Second and third equation guarantees that maximum number of input arc and output arcs are one. And the last three equations emphasize that it is integer programming problem where the values as 0 or 1. The objective function states to minimize the total cost.

Question. How can GA be used to solve the Generalized Traveling Salesman Problem?

This objective function and constraints above can be used as a way to determine the fitness function in the GA-based algorithm.

Now first comes the question of “How to represent a representative of solution, which is a chromosome?” Well, we can represent it as a pair, cluster number and the number of the city in that cluster.

Suppose there are 5 clusters and each of the cluster with 10 cities. Then a possible solution to G-TSP would be as follows:

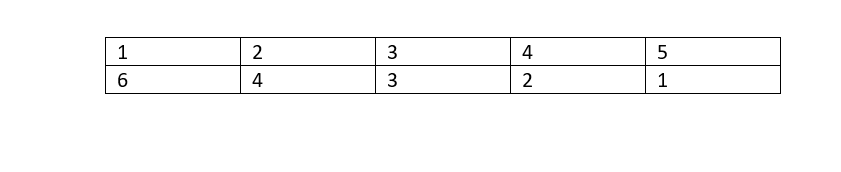
Here 6th city from cluster 1 takes part in solution, 4th city from cluster 2, third city from cluster 3, 2nd city from cluster 4 and 1st city from cluster 5.

Next, we need to determine the three operators of GA algorithm, which is selection, crossover, and mutation.

I. Selection. There are various ways to do selection, one is to duplicate the winning chromosomes in place of losing chromosomes. The work in [1] is based on removing the worst 10%. However, we choose to keep winning neurons.

II. Crossover. There are various kinds of crossover operators. Let us understand cycle crossover. The crossover starts from the left of the strings. The bits are exchanged and the duplicates in the string are removed using a cyclic approach. Duplicates need to be removed as this is a kind of permutation problem where all elements at the top of a row of the chromosome should be unique.

III. Mutation. Mutation in a permutation can be performed by randomly choosing a bit in the chromosome and flipping it with another bit from the sequence.

More on Genetic Operators in a separate post.

The results shown in this research paper [1] are quite encouraging. However, our approach in the above text is a bit different from what the authors of [1] have presented. We have not fully used the approach by [1] rather we were focussed on what the problem of G-TSP is and how to solve it with GA given the uniqueness of G-TSP.

Stay updated.

References

[1] Jafarzadeh, H., Moradinasab, N., & Elyasi, M. (2017). An enhanced genetic algorithm for the generalized traveling salesman problem. Engineering, Technology & Applied Science Research, 7(6), 2260–2265.