Summary: Do we need to now write from scratch for more mathematical structures? Yes or No, lets explore here. Or classes for more new mathematical structures can be generated by AI?

Some of the things I tried on SageMaths and ChatGPT. No need to install SageMaths. Try even new things. But how to run these, and how to verify codes, ChatGPT can you answer? I dont want to install it on system. Any web interface to run these would be help.

I have yet to verify these codes; I was excited to share this, but I am verifying it as of now. I am using AI to generate codes for Mathematics for the first time. Or are these codes on safemaths website? Sagemaths.org can you confirm?

Till the time I verify these, run these, I want to share with you what I learned,

— Are these codes there on documentation of sagemaths.org?

— Are these codes generated by chatGPT?

—Or these codes made by ChatGPT? Then it’s wonderful progress in research in mathematics.

— How to run these codes which are output by chatGPT to verify for correctness

— Here it created a class for semigroups, topology, general and special linear groups (an advance algebra research problem) as well.

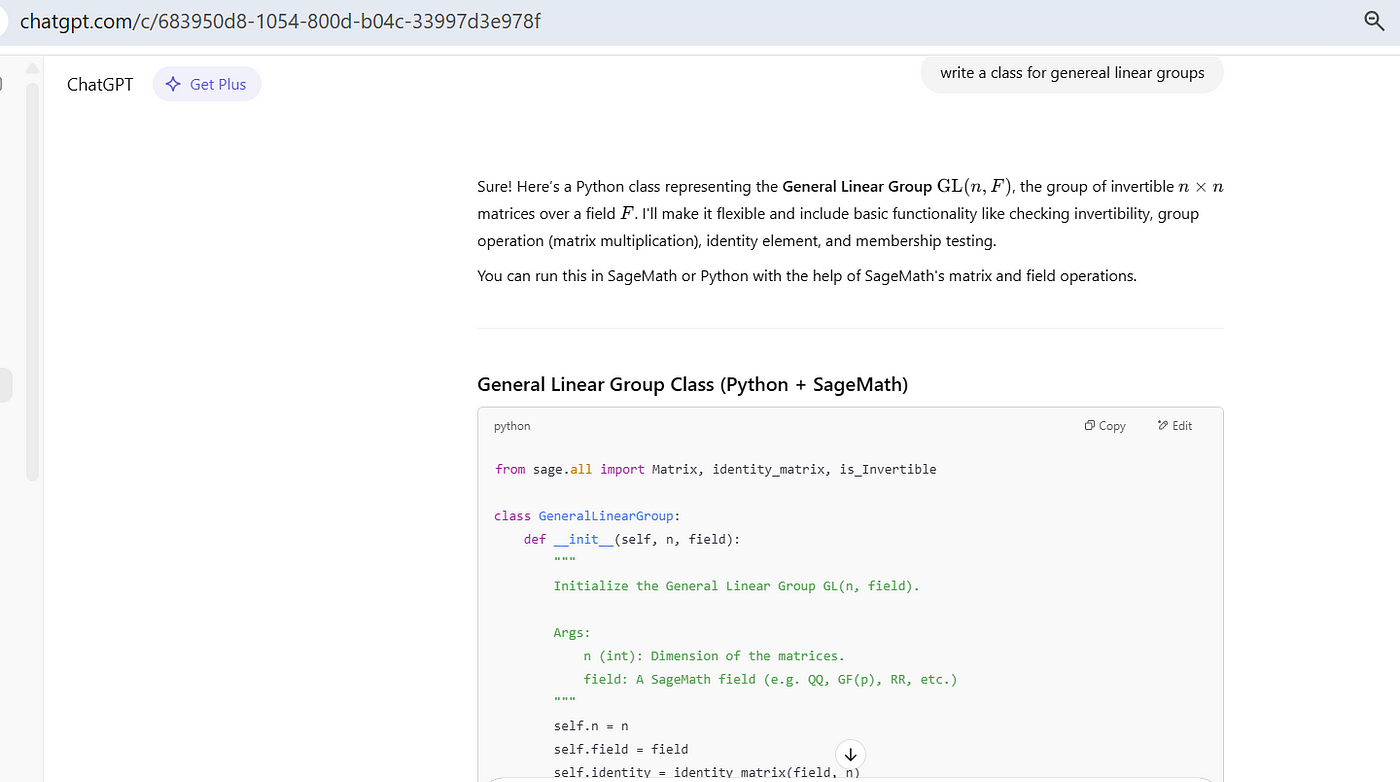
Here is my project area, General Linear Groups with SageMaths:

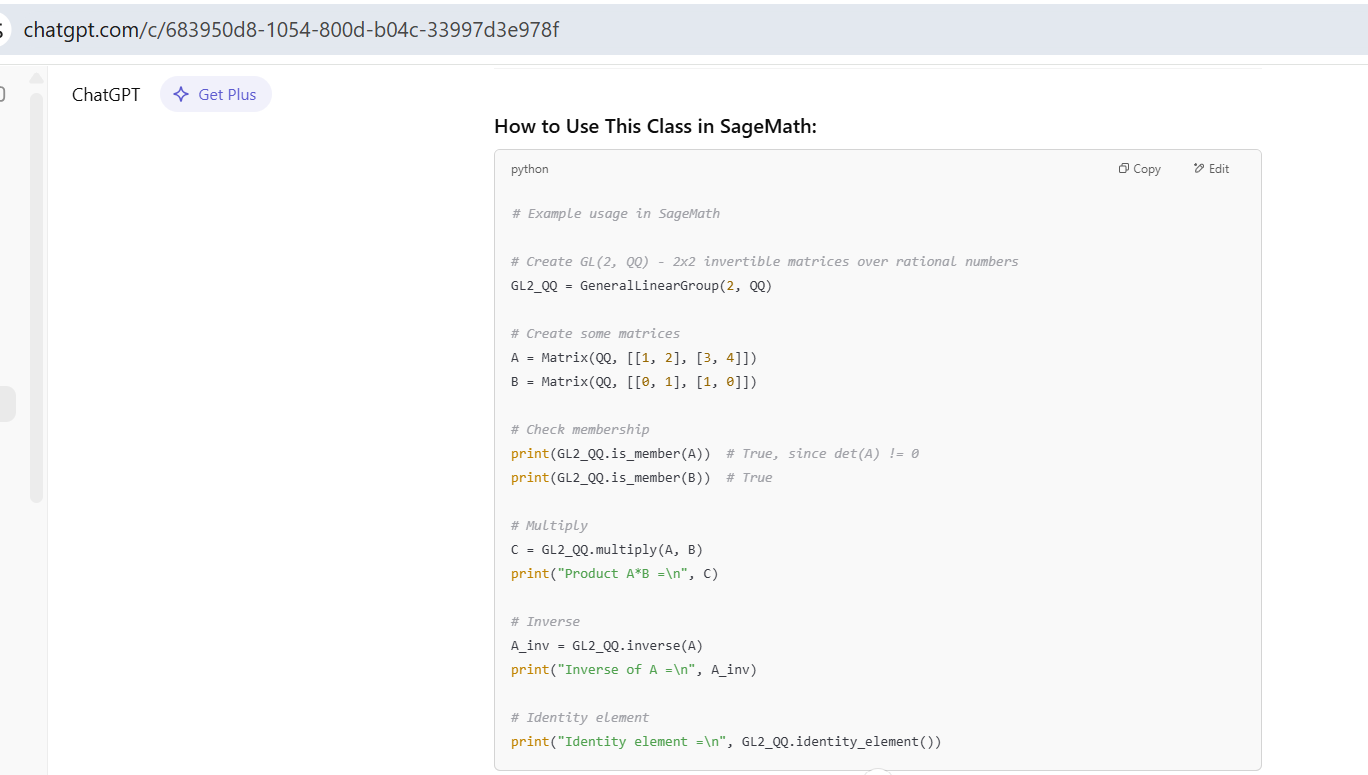
Write a class for general linear groups

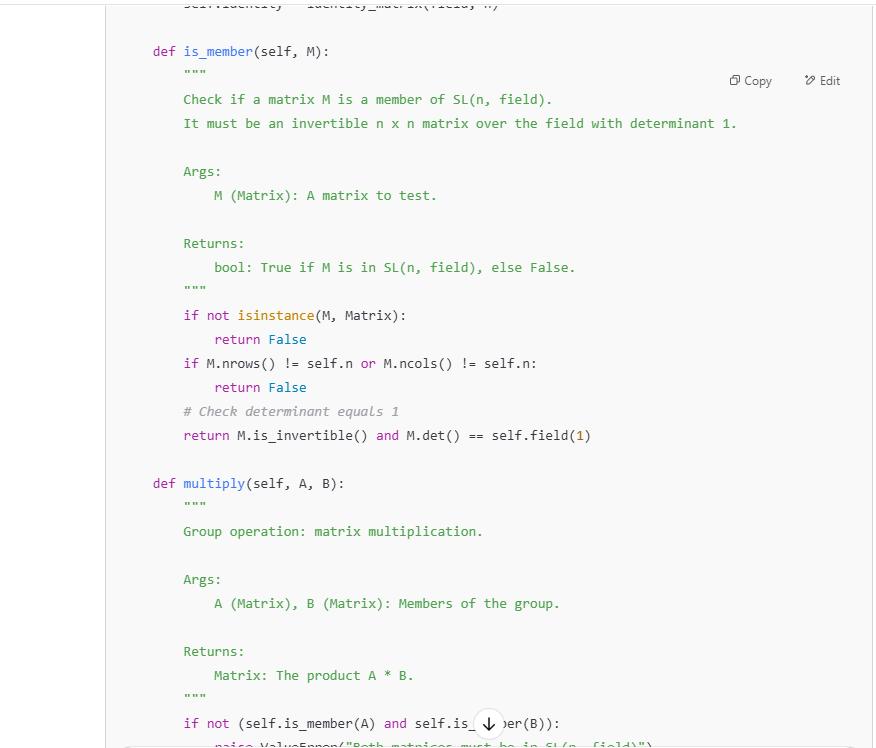
Write the class of special linear groups

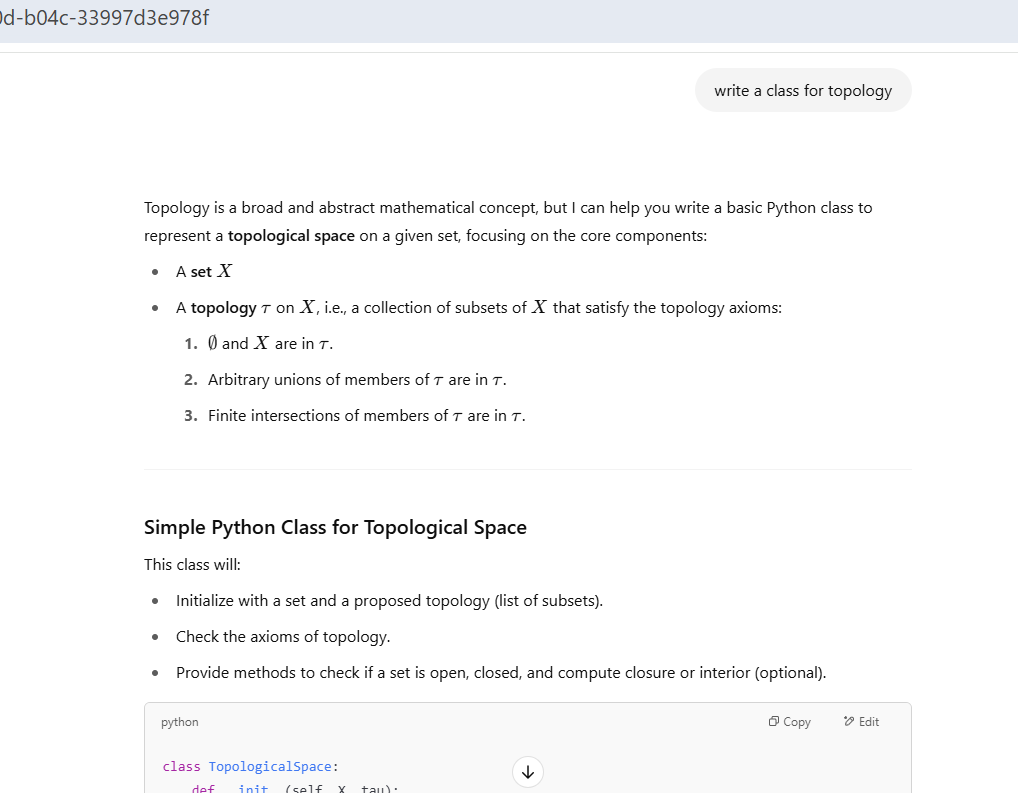
Then I tried Topology, an Analysis topic

write a class for topology

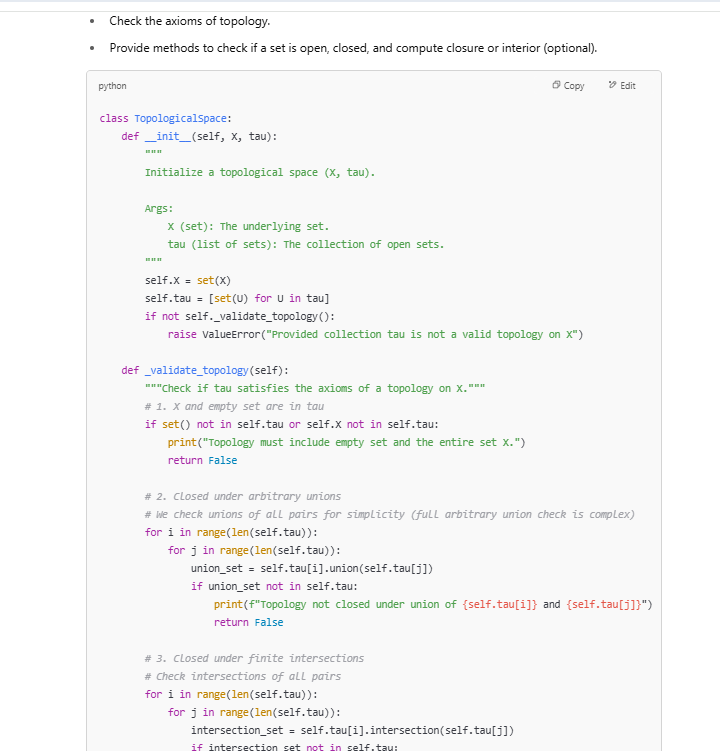
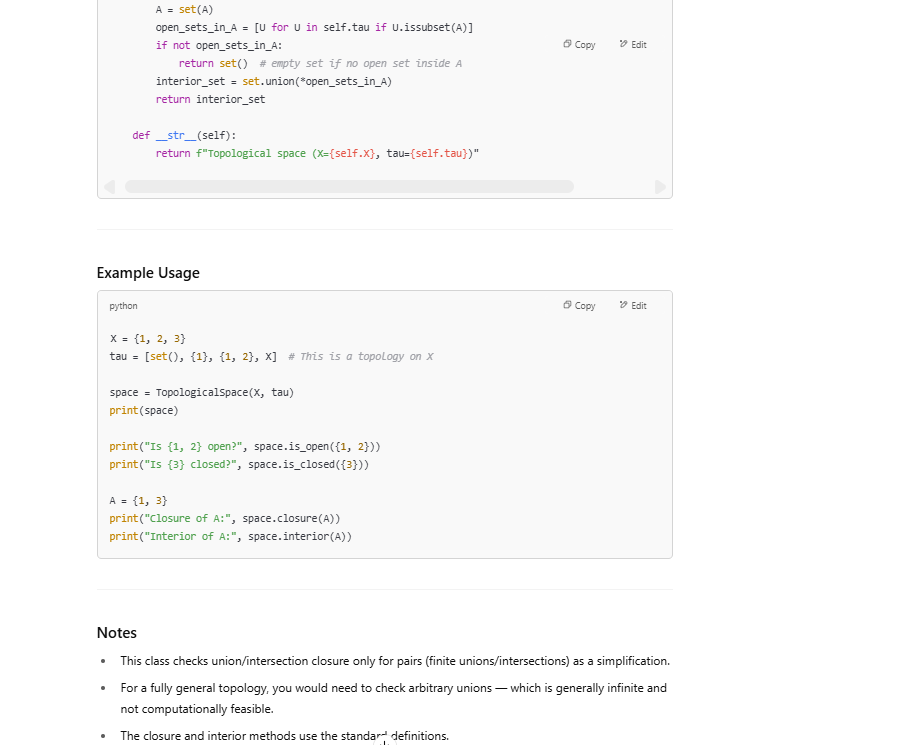
Note full code is not given for the above given space restrictions. Users can use same prompts to generate it.

Questions ?

— Can we refactor and write more codes with AI of chatGPT with sagemaths.org?

— How many more structures can be generate form here?

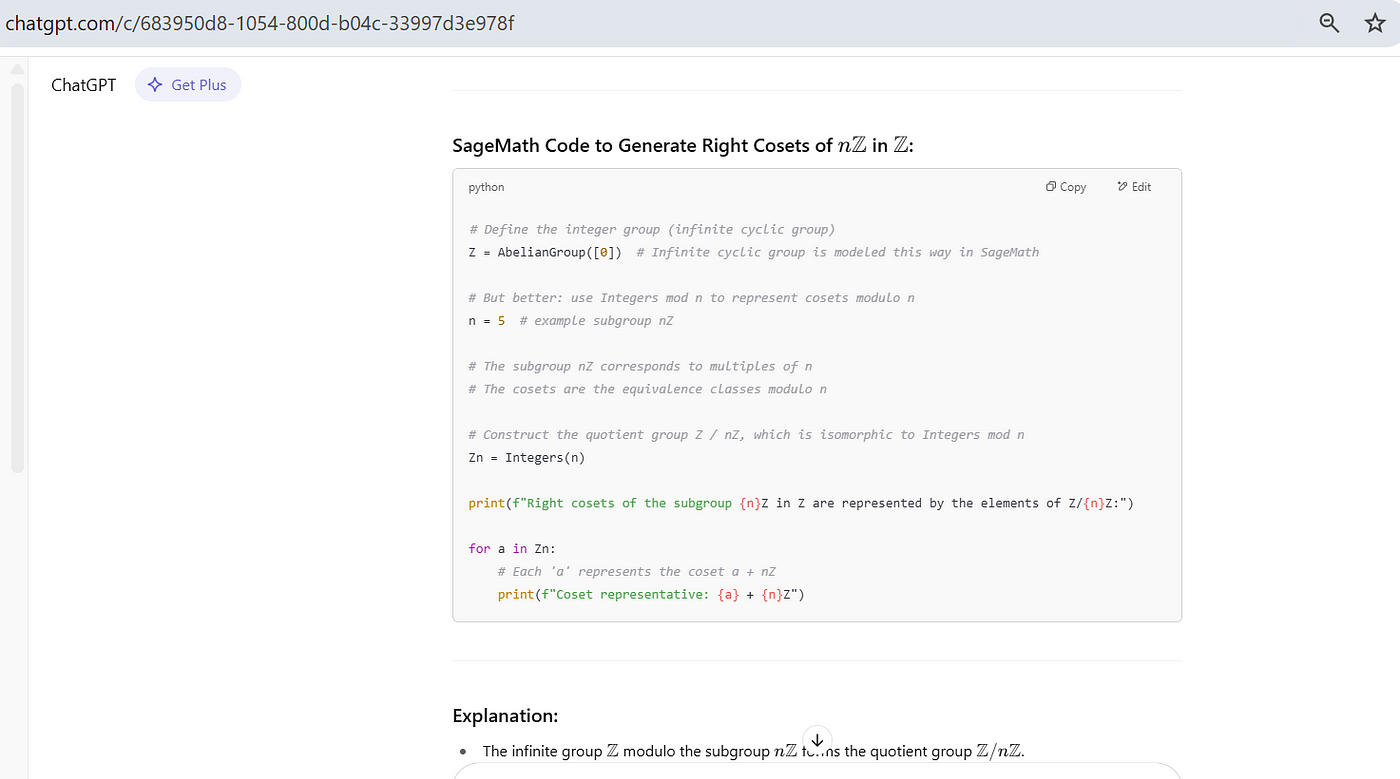
These codes can be used to generate more AI-based codes.

If all this goes well, theorems of Advanced Mathematics can be done with ChatGPT step by step.

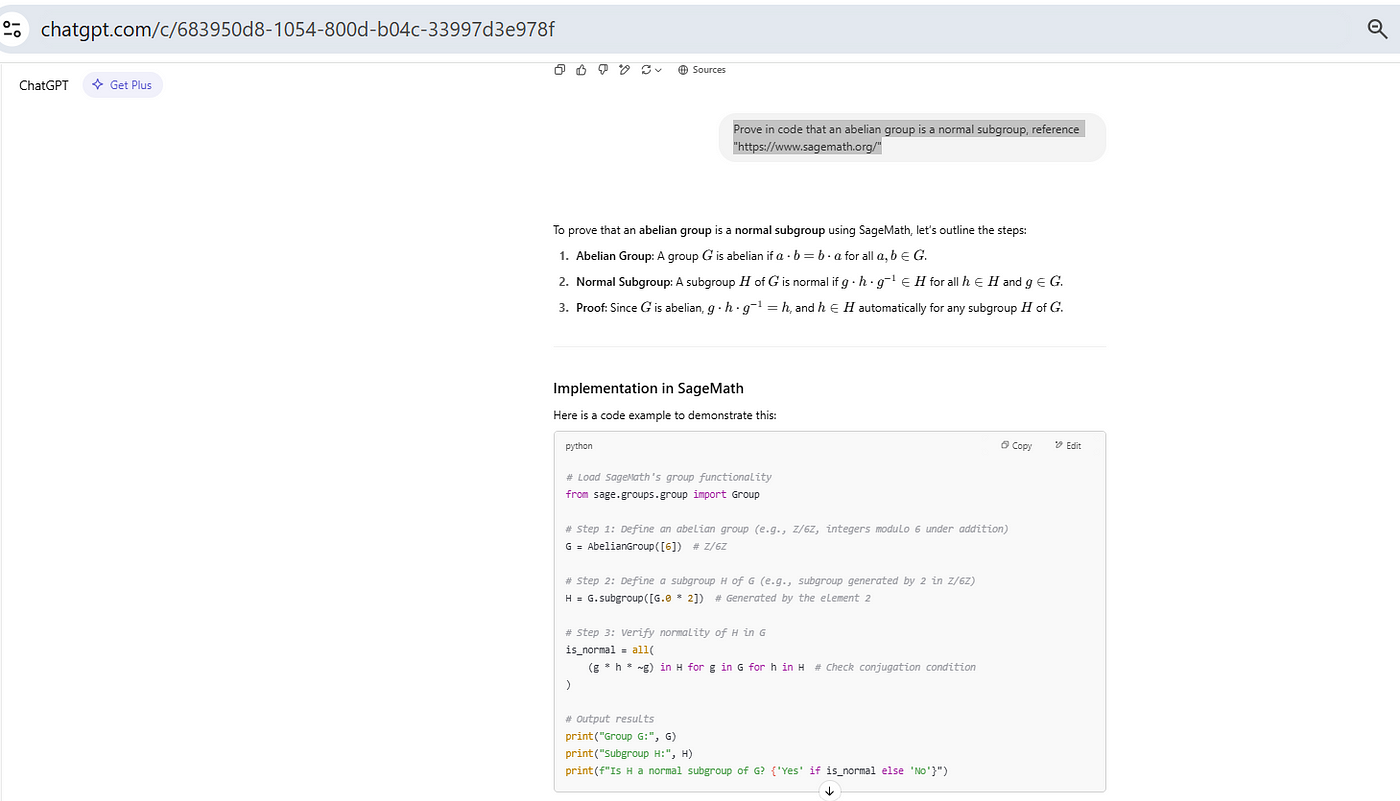
A. Prove in code that an abelian subgroup is a normal subgroup, reference “https://www.sagemath.org/”

B. Let T be a linear operator on the finite-dimensional space V. Let Ci, . . . , Ck be the distinct characteristic values of T and let Wi be the space of characteristic vectors associated with the characteristic value Ci. If W = sums of Wi, then, dim W = dim Wi +….)+ dim Wk.

C. The kernel of a group homomorphism is a normal subgroup

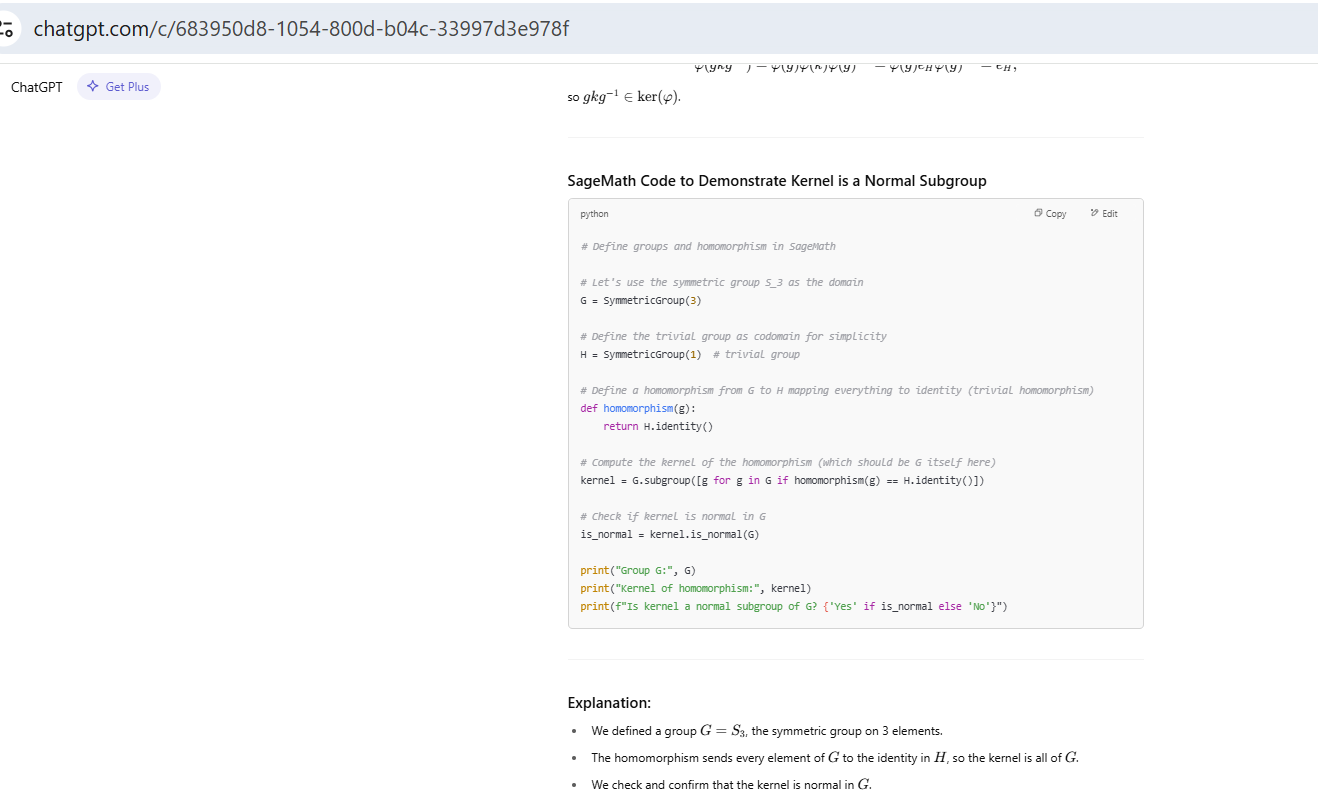
Some other coding examples on Abstract Mathematics:

I. Write a code to create matrix of linear transformation from “https://www.sagemath.org/”

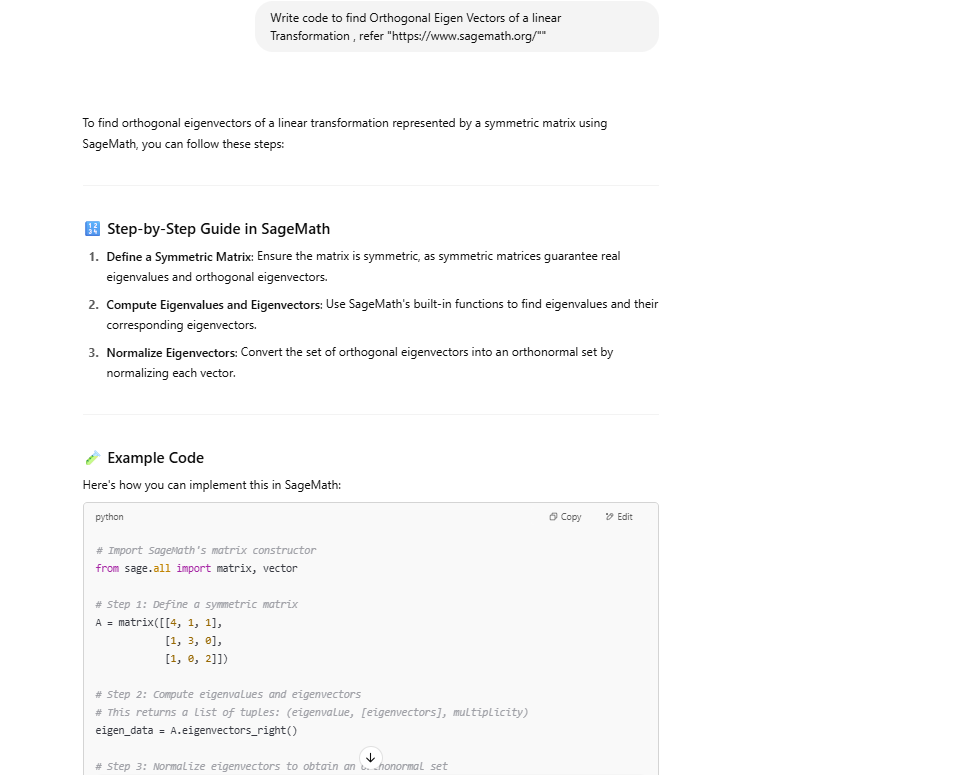
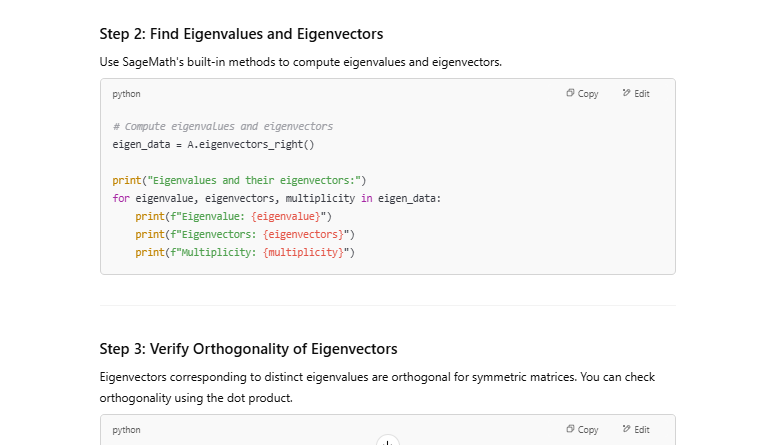
II. Write code to find Orthogonal Eigen Vectors of a linear Transformation , refer “https://www.sagemath.org/””

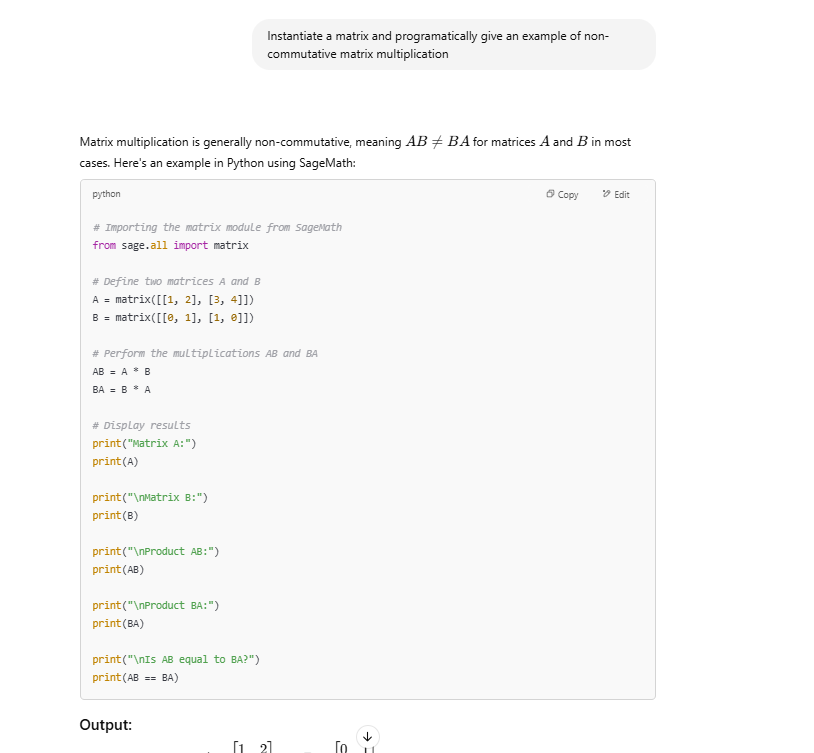
III. Instantiate a matrix and programatically give an example of non-commutative matrix multiplication

IV. Write the class code for semigroup from site “https://www.sagemath.org/

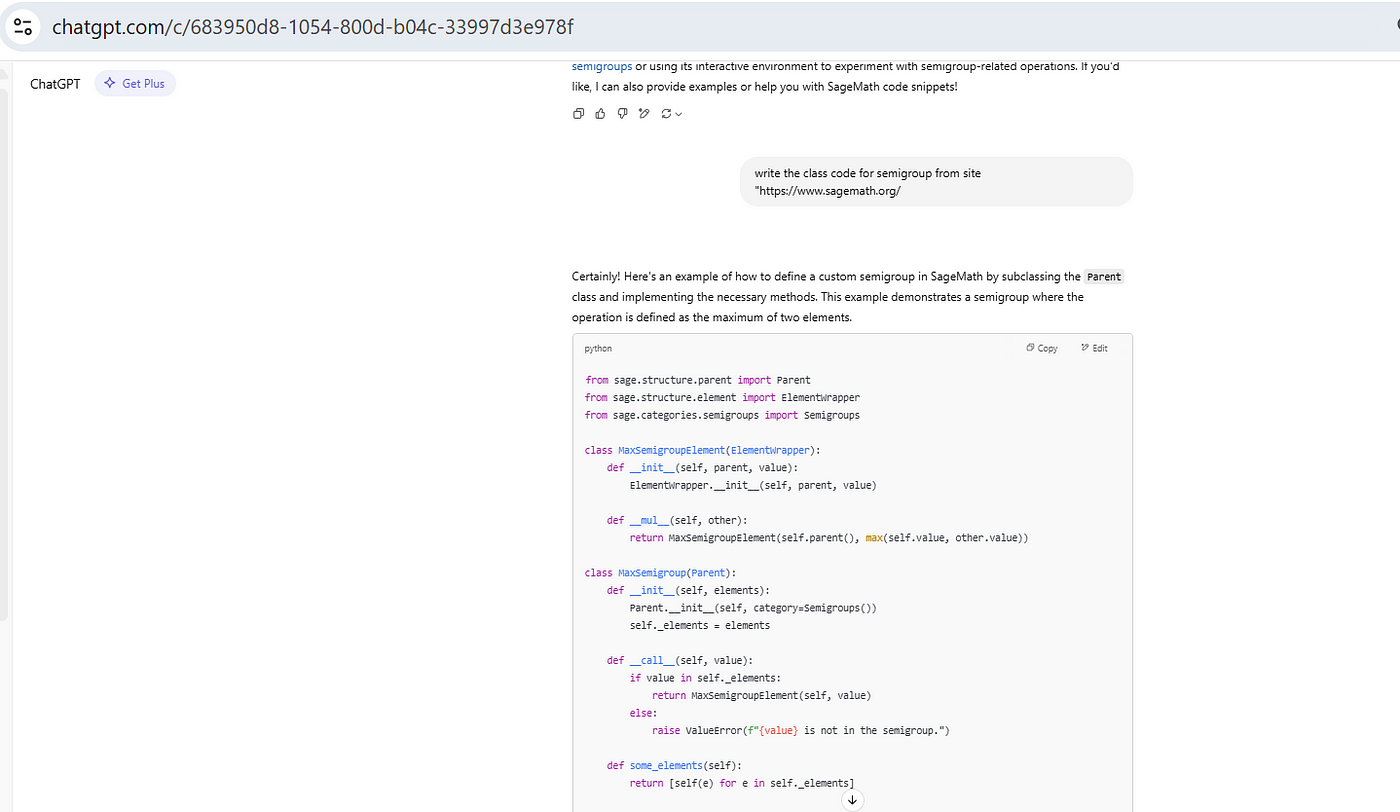
I have yet to verify these; I was just excited to share this, rather than verifying it right now.

Thanks for reading